Aspectos de la serie del 13
El armónico 13 divide el círculo de la eclíptica en trece partes iguales de 27,7 grados a partir de cero Aries y aloja en cada una de esas partes una copia comprimida de un zodíaco completo. El despliegue y la superposición de esos trece zodiacos en uno solo, arrastrando cada uno consigo los planetas o ángulos que contuviera su parte, da lugar a la carta del armónico 13. La división del círculo en trece partes iguales da lugar, también, a los aspectos de la serie del 13: el trecil (27º 42'), el bitrecil (55º 23'), el tritrecil (83º 05'), el tetratrecil (110º 46'), el pentatrecil (138º 27') y el hexatrecil (166º 09'). De acuerdo con la propuesta de John Addey, el orbe que corresponde a estos aspectos debe ser una treceava parte del que se asigne a la conjunción. Dos planetas que formen uno cualquiera de estos aspectos en la carta radical aparecerán en conjunción en la carta del armónico 13.
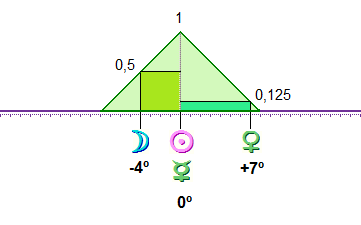
El valor de un trecil (27,7 grados) es prácticamente el mismo que el de la máxima elongación posible de Mercurio (27,8 grados). Se entiende por elongación de Mercurio su ángulo de separación con respecto al Sol, vistos ambos desde la Tierra.
Máxima elongación de Mercurio
Esto puede ser una simple coincidencia, pero también es posible que encierre algún significado. Todavía es muy poco lo que se sabe sobre el armónico 13 y sobre los aspectos de la serie ligada a él, de modo que sería prematuro tratar de buscar alguna semejanza entre la naturaleza astrológica de Mercurio y la de los treciles. Pero al menos podemos constatar un hecho interesante: la serie del 13 es la primera en la que Mercurio tiene la oportunidad de participar haciendo un aspecto partil con el Sol distinto de la conjunción.
En efecto, si en una carta del armónico 13 encontramos al Sol en conjunción con Mercurio, esto puede significar dos cosas:
(A) El Sol y Mercurio ya estaban en conjunción en la carta radical (con un orbe trece veces más pequeño).
(B) El Sol y Mercurio estaban el trecil en la carta radical.
En cualquiera de los doce armónicos anteriores, la única opción posible sería la (A). Por tanto, de alguna manera, Mercurio alcanza su independencia con respecto al Sol y su "mayoría de edad" a partir del armónico 13 ó, más bien, de los aspectos asociados a este armónico. En efecto, tal como ya he dicho, Mercurio no se aleja nunca lo suficiente del Sol como para poder hacer ningún aspecto de la serie del 12, ni del 8, que son las más usadas, -fuera de la conjunción, que pertenece a todas las series. Ni tampoco de las series del 5, del 7 y del 9, que últimamente se están usando un poco más.
La conjunción de Mercurio con el Sol parece un tanto desequilibrada, en el sentido de que no se da entre dos planetas igual de poderosos. En ella Mercurio se ve relegado indefectiblemente a un papel subordinado, como si no tuviera naturaleza propia y sólo le quedara la opción de servir de portavoz del Sol. En el trecil, sin embargo, Mercurio ocupa un lugar propio, puede tener su propia posición y expresarla frente a la posición del Sol. Así abandona la posición infantil de total dependencia del padre.
Una manera de aprender algo sobre el armónico 13 es usarlo como armónico de la edad. Sobre este tema he hablado ya bastante en este blog de Cadencias microcósmicas, especialmente en la entrada del 15 de marzo de 2010 (Armónicos de la edad) y en las siguientes. Tal como expliqué entonces, la carta del armónico 13 puede usarse como representativa de la edad de 12 años, porque la carta radical, que es el armónico 1, funciona desde el nacimiento; entonces, sumando un armónico por año a la carta radical, tendremos 13 armónicos a los 12 años. Así entendida, esta técnica ha sido denominada armónicos de la edad + 1. Hay también algunas buenas razones para esperar que la carta del armónico 13 represente la edad de 13 años, y algunos astrólogos, como Dymock Brose, se muestran no ya satisfechos sino incluso entusiasmados con los resultados de esta segunda manera de enfocar el asunto, que se conoce como armónicos de la edad, sin más. Personalmente he obtenido algunos resultados interesantes trabajando de la forma en que lo hace Brose, pero los más contundentes que he hallado se corresponden casi siempre con la otra fórmula (edad + 1). Creo, por tanto, que el armónico 13 adquiere protagonismo ya desde los 12 años, con independencia de que a los 13 pueda tener una segunda oportunidad de manifestarse.
La edad de 12 años ha sido señalada como crucial por la Psicología Evolutiva, lo que convierte al armónico 13 en una carta de especial relevancia. A esa edad se completa la adquisición de todas las habilidades relacionadas con el lenguaje, termina la infancia y comienza la pubertad (o prepubertad). Se acelera el crecimiento y se desarrollan las características sexuales secundarias. Se adquiere la capacidad de pensamiento independiente y crítico. Según Piaget, a los 12 años comienza la etapa de las operaciones formales. Esto significa que el adolescente es capaz de pensar en todas las maneras posibles de interpretar una situación o solucionar un problema; es decir, es capaz de formular un conjunto de hipótesis y calibrarlas para escoger la más viable. Su estilo de pensamiento se parece al de un científico y es capaz de emplear la deducción lógica en ausencia de estímulos sensoriales. Busca reglas abstractas que le permitan resolver problemas, de un modo racional y sistemático. Por primera vez, el niño es capaz de preguntarse quién es él mismo, cuál es su lugar propio en la vida o en la sociedad, qué planes de futuro puede hacer y si las reglas de comportamiento aprendidas son realmente valiosas o encierran alguna falsedad.
Del mismo modo que Mercurio en trecil con el Sol, el adolescente cobra conciencia de su existencia separada. Las habilidades lingüísticas, lógicas y de pensamiento crítico que se alcanzan a esta edad guardan una íntima relación con las características que los astrólogos asocian con Mercurio, planeta que también ha sido ligado tradicionalmente con la adolescencia. Más recientemente, Bruno Huber ha señalado la edad de 12 años como la de la entrada del Punto de la Edad en la casa 3, que guarda analogías con Géminis y con Mercurio.
Entre los antiguos israelitas, se consideraba la edad de 12 años como aquella en que los niños pasaban de ser hijos de sus padres a ser "hijos de la Ley escrita" (Mercurio), quedando desde entonces obligados por ella. Es la edad en la que Jesús se pierde en Jerusalén y es hallado al cabo de tres días en el templo, discutiendo con los doctores y maravillando a todos con su sabiduría y sus respuestas.
Por tanto, no sería de extrañar que las personas con cartas del armónico 13 fuertes estuvieran especialmente dotadas para el desarrollo de habilidades lógicas, lingüísticas o matemáticas y puedan destacar como expertos en lenguajes de programación de ordenadores o como jugadores de ajedrez. Y en efecto, algunos notables personajes en estas áreas tienen cartas del armónico 13 muy marcadas. Es especialmente interesante el caso de Bobby Fisher, no sólo por haber sido uno de los más legendarios campeones del mundo de ajedrez, sino también porque su eclosión tuvo lugar hacia los 13 años de edad. Sobre él escribió Pablo Morán (Los niños prodigio del ajedrez, p.94) : "Como niño prodigio no fue muy brillante; en cambio, como adolescente prodigio no ha tenido parangón en la historia del ajedrez".
9 de Marzo de 1943, 19h 39m GMT
Chicago, 87W39, 41N52
El armónico 13 de Bobby Fisher contiene una excepcional configuración de Grandes Trígonos que enlazan a Urano con Plutón, Neptuno, Venus, Mercurio y Marte, además del MC armónico superpuesto al FC radical.
Otro personaje que destacó como uno de los principales padres de la lógica formal contemporánea y excelente filósofo del lenguaje fue Ludwig Wittgenstein. Su armónico 13 está cargado de aspectos tensos, especialmente una doble oposición de Saturno/Marte a Sol/Plutón, superpuesta al eje MC-FC armónicos y cuadrando a Venus.
26 de abril de 1889, 19h 24m GMT
Viena, 16E20, 48N13
También su pensamiento evolucionó en medio de agudos contrastes, hasta el punto de que se suele hablar de un Wittgenstein I, autor del Tractatus Logico-Philosophicus, y de un Wittgentein II, que cuestiona sus propias tesis del Tractatus en sus posteriores Investigaciones filosóficas. Participó en la Primera Guerra Mundial, y las primeras formulaciones de sus ideas del Tractatus fueron redactadas en un cuaderno que llevaba consigo en las mismas trincheras del campo de batalla.
Dentro del mundo de la informática podemos mencionar a Bill Gates, cuyo armónico 13 reúne cinco planetas alrededor de su Ascendente: La Luna, Venus, Júpiter, Plutón y Saturno; aunque destacó mucho más como hábil negociante que como virtuoso de la programación. Pero eso es también propio de Mercurio.
Por supuesto, lo que aquí planteo no pasa de ser una sugerencia. Se necesitará una investigación más amplia y sistemática antes de decidirse a aceptarla o rechazarla. Cualquier observación al respecto será bienvenida.
© Julián García Vara, octubre, 2010.