Los armogramas de O'Neill

Un armograma es un gráfico que representa la evolución de la intensidad de uno o de varios armónicos a lo largo de un periodo de tiempo. Naturalmente, sólo es posible hacer esto si se resuelve previamente de algún modo el problema de cuál es la mejor manera de determinar la magnitud de la intensidad de una carta armónica. Ya he discutido las líneas maestras de este asunto en las entradas anteriores de este blog. Recordemos que hay, básicamente, dos soluciones formales: el recuento de aspectos y la suma de vectores. Cualquiera de estas dos técnicas puede servir para diseñar un armograma y, de hecho, se han utilizado ambas; pero como no miden exactamente lo mismo, conviene estar informado del método que se está usando en cada caso.

El método del recuento de aspectos consiste simplemente en contar el número de conjunciones que hay en una carta armónica. Aparentemente, nada puede ser más fácil que esto, pero como ya señalé en la entrada del pasado 10 de septiembre titulada Armónicos fuertes y débiles, incluso una tarea tan sencilla como ésta puede estar sembrada de dificultades. De todas las que ya enumeré en el mencionado artículo, cabe destacar cuatro:

1) ¿Qué planetas o factores de una carta astral deben admitirse como legítimos integrantes de conjunciones computables?

2) ¿Qué orbe se debe utilizar?

3) ¿Qué modelo de aspectos debe guiar la cuantificación de la intensidad de la carta?

4) ¿Deben ignorarse las conjunciones de una carta armónica n que estaban ya presentes en la carta radical (A1)?

Mike O'Neill, que, al parecer, fue quien introdujo el término "armograma" (harmogram), diseñó un pequeño programa para calcularlos y dibujarlos en el cual deja que sea el propio usuario quien decida qué solución dar a cada uno de esos cuatro problemas. El programa de Mike O'Neill puede obtenerse gratuitamente en la página siguiente:

http://www.astrovdm.com/harmogrm.htm

Es un programa al viejo estilo MS-DOS, que puede que no funcione en algunos equipos recientes (por ejemplo, los que utilizan Windows Vista). En ese caso, la solución es usar un emulador de MS-DOS, como, por ejemplo, el DOSBox.

Cuando ponemos en marcha este programa, lo primero que veremos será lo siguiente:

DEFAULT SETTINGS (0/1)

El cero equivale a "no" y el uno equivale a "sí". Por tanto, si deseamos atenernos a las opciones "por defecto" introduciremos un uno (1). En ese caso, el programa utilizará un orbe de 12 grados, usará 10 planetas (Sol, Luna, Mercurio, Venus,, Marte, Júpiter, Saturno, Urano, Neptuno y Plutón), excluirá del recuento aquellas conjunciones que ya estaban presentes en la carta radical (A1) y utilizará un modelo de orbe gaussiano. Si éstas no son nuestras opciones predilectas, introduciremos un cero (0) y el programa nos dará la oportunidad de modificarlas.

El orbe de 12 grados, que a primera vista puede parecer un poco amplio, en realidad se queda más bien corto. Implica que a las oposiciones se les concederá un orbe de 6 grados, a los trígonos 4 grados, a las cuadraturas 3 grados y a los sextiles 2 grados. Estos orbes están por debajo de los que normalmente utiliza la mayoría de los astrólogos.

Espero no desorientar a nadie con lo que acabo de decir. No es que los armogramas de O'Neill tengan en cuenta todos esos aspectos en cada una de las cartas armónicas. Se limitan, como ya he dicho, a contabilizar conjunciones. Ahora bien, si asumimos para la conjunción un orbe de 12 grados, las conjunciones que encontremos en el armónico 2 procederán de aquellas conjunciones y oposiciones de la carta radical (A1) que no excedan del orbe de 6 grados. Y si excluimos del recuento de conjunciones del armónico 2 aquellas que ya lo eran en el armónico 1, el número de conjunciones restantes será igual al número de oposiciones de la carta radical dentro del orbe de 6 grados. De ese modo, se puede usar el armónico 2 para rastrear oposiciones, así como el armónico 3 para rastrear trígonos, el armónico 5 para contabilizar quintiles y biquintiles, etc.

Esta es una de las razones por las cuales el programa de O'Neill, usando las opciones por defecto, no contabiliza las conjunciones de cada armónico que ya lo eran en la carta radical. Si queremos investigar la naturaleza de los aspectos de la serie del Siete (septiles, biseptiles y triseptiles) seleccionando cartas que contengan muchas conjunciones en el armónico 7, sin tomar la precaución de mirar cuántas de estas conjunciones lo eran ya en el armónico 1, entonces corremos el riesgo de tomar como representativas de la naturaleza de los aspectos de la serie del Siete algunas cartas radicales que no contengan ningún septil ni biseptil ni triseptil, o que contengan muy pocos. Sin embargo, la función principal de un armograma es medir la fuerza o intensidad de un armónico y de la serie de aspectos que va asociada al mismo, no su naturaleza. Explicaré un poco más abajo por qué no me parece buena idea excluir ninguna conjunción presente en cualquier carta armónica, por más que pudiera estar también en la carta radical o en algún otro armónico primo más bajo. Pero primero debo decir algo sobre los distintos modelos de orbes de aspectos entre los que hay que elegir antes de abordar la tarea de cuantificar la fuerza de una carta armónica.

1) MODELO DE ORBE "TODO O NADA"

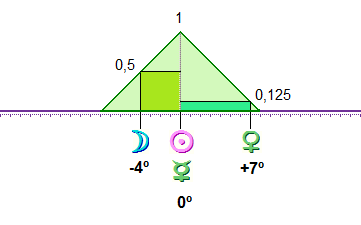
En este modelo, cualquier conjunción entre dos planetas recibe un punto, sin que importe si la conjunción es partil o se halla cerca de un extremo del orbe admitido. Supongamos que optamos por un orbe de 8 grados y que encontramos una carta que contiene una conjunción exacta del Sol con Mercurio (0 grados de distancia), estando la Luna 4 grados antes y Venus 7 grados después de Sol/Mercurio. Este grupo de planetas incluye un total de cinco conjunciones dentro de un orbe de 8 grados: Sol/Mercurio, Sol/Luna, Mercurio/Luna, Sol/Venus y Mercurio/Venus. Por tanto, contribuirá con cinco puntos a la valoración total de la carta que lo contenga.

Modelo de orbe "todo o nada"

2) ORBE DE PROGRESIÓN LINEAL

En este modelo, toda conjunción partil (distancia 0 grados) recibe un punto. Las demás conjunciones reciben tan sólo una parte de un punto inversamente proporcional a su distancia a la conjunción partil. Siguiendo con el ejemplo anterior, la conjunción Sol/Mercurio recibirá un punto completo. Las conjunciones Sol/Luna y Mercurio/Luna están a una distancia de 4 grados, que representa la mitad del orbe admitido; por tanto, recibirán medio punto cada una. Las conjunciones Sol/Venus y Mercurio/Venus están a una distancia de 7 grados, que representa 7/8 del orbe admitido; por tanto, recibirán un octavo de punto cada una. En total, este grupo de planetas contribuirá con 2,25 puntos a la valoración de la carta.

Modelo de orbe de progresión lineal

3) ORBE GAUSSIANO O DE PROGRESIÓN SINUSOIDAL

En este modelo, al igual que en el anterior, se considera que los aspectos incrementan progresivamente su intensidad desde el extremo inferior del orbe hasta el punto de conjunción partil, y después pierden progresivamente intensidad hasta llegar a cero en el extremo opuesto del orbe. Sin embargo, aquí se entiende que la progresión no sigue un ritmo lineal, sino que se ajusta a una curva normal o campana de Gauss. También aquí la conjunción Sol/Mercurio recibirá un punto completo, pero las conjunciones Sol/Luna y Mercurio/Luna recibirán aproximadamente un cuarto de punto, y las conjunciones Sol/Venus y Mercurio/Venus apenas un 0,01. En total, en este modelo el grupo planetario alcanzará una puntuación de alrededor de 1,52 puntos.

Modelo de orbe gaussiano

A estas alturas ya debe estar bastante claro que un armograma para un armónico n y para una fecha y hora determinadas puede llegar a tener una apariencia muy distinta dependiendo del número de planetas usado para calcularlo, de la magnitud del orbe asignado a una conjunción, del modelo de orbe escogido y de la decisión de excluir o no aquellas conjunciones que ya estaban presentes en la carta radical o en algún otro armónico primo anterior. No sólo varía la apariencia del armograma del armónico n en función de los parámetros escogidos, sino que también se altera la jerarquía entre los diferentes armónicos; es decir, el armónico dominante puede ser uno u otro dependiendo de las opciones por las que nos decantemos.

Ahora podemos volver a considerar la cuestión de si debemos contabilizar o no todas las conjunciones presentes en una carta armónica, con independencia de su "pasado armónico". Supongamos que deseo medir el nivel de decibelios a que está sometida mi vivienda en un momento determinado. Digamos que en el exterior hay unos obreros levantando el pavimento con una taladradora para reparar las tuberías del agua y que he decidido poner música alta para que el ruido de la calle no me moleste tanto. El medidor de decibelios en el interior de mi vivienda registrará la intensidad de todo el ruido que se oye en ella, sin que importe para nada si procede del exterior o se origina en el interior. De manera similar, contabilizar todas las conjunciones presentes, por ejemplo, en una carta del armónico 7, nos da la intensidad total de ese armónico, porque las conjunciones del armónico 7 que ya estaban presentes como tales en la carta radical son conjunciones que todavía se escuchan en el armónico 7. Para algunos propósitos puede ser importante distinguir entre el ruido que se origina fuera de la vivienda (las conjunciones que ya estaban en la carta radical) y el que se origina en el interior de la misma (las conjunciones que surgen por primera vez en el armónico 7), pero no para medir la intensidad total de los decibelios (la intensidad del armónico 7). Además, si se usa un modelo de orbe de progresión lineal, cualquier conjunción del armónico 7 que estuviera ya presente en la carta radical tendrá un orbe siete veces mayor que el que tenía en la carta radical, de modo que recibirá una puntuación siete veces menor que en aquella, o incluso mucho menor aún si usamos orbes gaussianos. Esto relega automáticamente a segundo plano ese tipo de conjunciones.

El programa de armogramas de O'Neill incluye los tres modelos de orbes descritos más arriba. El modelo "todo o nada" se usa en la parte inferior de cada gráfico y uno de los otros dos -el de progresión lineal o el gaussiano, a elección del usuario- se usa en la parte superior. Vamos a calcular uno de estos armogramas, para que podamos ver el resultado. Usaremos para ello los datos natales de Albert Einstein.

En DEFAULT SETTING escogeremos cero (0) para decidir nuestras propias opciones. Entonces veremos esto:

LAST PLANET (PL=10) (NN=11)

Si introducimos 10 usará todos los planetas hasta Plutón. Si introducimos 7, sólo llegará hasta Saturno. Introduciendo 11 usará los 10 planetas más el Nodo Norte de la Luna. En esta ocasión escogeremos 11. Entonces nos preguntará si deseamos incluir la Luna. Le diremos que sí (1). A continuación nos pregunta si deseamos incluir aquellas conjunciones que ya estaban en la carta radical. También responderemos que sí (1). Entonces nos ofrecerá la posibilidad de usar un modelo de orbe gaussiano. También le diremos que sí (1). Después nos pedirá que asignemos el número de grados al orbe. Usaremos, por ejemplo, 18. Lo siguiente es dar un nombre al armograma. Le llamaremos ALBERT EINSTEIN. Introducimos sus datos natales (14,3,1879 10.50 GMT) y, a continuación nos preguntará para cuantos días antes y después de la fecha introducida queremos calcular el armograma (no olvidemos que los armogramas se calculan para un periodo de tiempo, no para un momento puntual). En este ejemplo, usaremos 9 días de margen. Entonces nos pedirá un intervalo de horas. Digamos que escogemos 6 horas. En ese caso, el programa calculará una carta cada 6 horas, partiendo de la fecha y hora central (las de nacimiento de Einstein, en nuestro ejemplo) hacia adelante y hacia atrás en el tiempo, hasta cubrir el margen de 9 días antes y otros 9 días después que hemos escogido. En total, 4 cartas diarias durante 18 días, 72 cartas. Por último nos pedirá el número del armónico para el que queremos calcular el armograma. Optaremos por el 7. Entonces nos volverá a pedir el número del armónico. No se trata de una confirmación. Si escribimos otro número de armónico sumará la intensidad del armónico 7 con la de ese otro número, pero eso no nos interesa. Así que introducimos cero (0) para indicarle que no calcule más armónicos. El programa realizará un recuento de conjunciones, tanto por el método de todo o nada como por el de orbe gaussiano en cada una de las 72 cartas, en orden cronológico. Por último, representará gráficamente la variación de intensidad del armónico 7 a intervalos de 6 horas durante esos 18 días, usando coordenadas cartesianas (el tiempo en las abcisas, la intensidad en las ordenadas). Mediante una línea continua representará las oscilaciones de intensidad, según el orbe gaussiano y mediante un histograma mostrará el número de conjunciones halladas en cada intervalo.

He aquí el resultado:

Se aprecia inmediatamente que con los parámetros que hemos escogido Albert Einstein nació en un momento en el que el armónico 7 se aproximaba a un pico máximo de intensidad dentro del periodo estudiado (18 días). Esto puede no ser así si escogemos otras opciones. Con el orbe utilizado (18 grados) los septiles, biseptiles y triseptiles de la carta radical que han sido tomados en cuenta son los que quedaban dentro de un orbe de 2º 34'. Pero la intensidad del armónico 7 sería aún mayor si tuviéramos en cuenta que el Ascendente forma aspectos de la serie del 7 con la Luna y con Urano, algo que el programa no considera, pero que acercaría aún más el pico del 7 a su hora de nacimiento.

Mike O'Neill y Nick Kollerstrom han mostrado gráficos similares a éste, con fuertes picos en el armónico 7, correspondientes a los momentos exactos en que se produjeron algunos importantes descubrimientos científicos, como los rayos laser o la penicilina. (Nick Kollerstrom, Mike O'Neill, The Eureka Effect: Astrology of Scientific Discovery, 1996).

© Julián García Vara, octubre 2010.